1. Prove or disprove the claim that there are integers m, n such that is a perfect square.
Proof: Let n = 0. Then . And is a perfect square. Q.E.D

2. Prove or disprove the claim that for any positive integer m there is a positive integer n such that is a perfect square.
Proof: For any positive integer m, let n=m+2, then . And is a perfect square. Q.E.D

3. Prove that there is a quadratic , with positive integers coefficients b, c, such that f(n) is composite (i.e, not prime) for all positive integers n, or else prove that the statement is false.
Proof: Let b=2 and c=1. Then . And and is composite for all positive integers n. Q.E.D

4. Prove that if every even natural number greater than 2 is a sum of two primes (the Goldbach Conjecture), then every odd natural number greater than 5 is a sum of three primes.
Proof: And since , so . And is odd for all natural numbers . Let . Then we can get . So now we have proven “if every even natural number greater than 2 is a su m of two primes, then every odd natural number greater than 5 is a sum of three primes.”

5. Use the method of induction to prove that the sum of the first n odd numbers is equal to .
Proof: We need to prove by induction.
For k=0, the left-hand side is 1 and the right-hand side is , so the identity is valid for k=0.
Assume the identity holds for k. So . Now we need to show show that . We split the into two sections i.e. . And by our assumption, we can get . It’s trivial to get . This is the identity for k+1. Hence, by induction, the theorem is proved.

6. The notation is a common abbreviation for the sum . For instance, , denotes the sum . Prove by induction that:
Proof: By induction.
For n=1, the left-hand side is 1 and the right-hand side is , so the identity is valid for n=1.
Assume the identity holds for n. So . Now we need to show show that . We split the into two sections i.e. . And by our assumption, we can get . It’s trivial to get . By addition of fractions, we can get . By combining like terms, we can get . Finally by factorization, we can get . This is the identity for n+1. Hence, by induction, the theorem is proved.

OPTIONAL PROBLEMS

1. In the lecture we used induction to prove the general theorem


1+2+...+n=12n(n+1)1 + 2 + . . . + n = \frac{1}{2}n(n + 1)

There is an alternative proof that does not use induction, famous because Gauss used the key idea to solve a “busywork” arithmetic problem his teacher gave to the class when he was a small child at school. The teacher asked the class to calculate the sum of the first hundred natural numbers. Gauss noted that if

1+2+...+100=N1 + 2 + . . . + 100 = N

then you can reverse the order of the addition and the answer will be the same:

100+99+...+1=N.100 + 99 + . . . + 1 = N.

So by adding those two equations, you get

101+101+...+101=2N101 + 101 + . . . + 101 = 2N

and since there are 100 terms in the sum, this can be written as

100⋅101=2N100 · 101 = 2N

and hence

N=12(100⋅101)=5,050.N = \frac{1}{2} (100 · 101) = 5, 050.

Generalize Gauss’s idea to prove the theorem without recourse to the method of induction.
Proof: Assume that . Then we can get . So by adding those two equations, we can get . and since there are n terms in the sum, this can be written as and hence

2. Prove that for any finite collection of points in the plane, not all collinear, there is a triangle having three of the points as its vertices, which contains none of the other points in its interior.
Proof: By contradiction.
Assume that for any finite collection of points in the plane, not all collinear, every triangle having three of the points as its vertices contain at least one point in its interior. Now we can easily construct a counterexample to our assumption. We construct a triangle having three vertices labeled A, B, and C, and a point D in its interior. 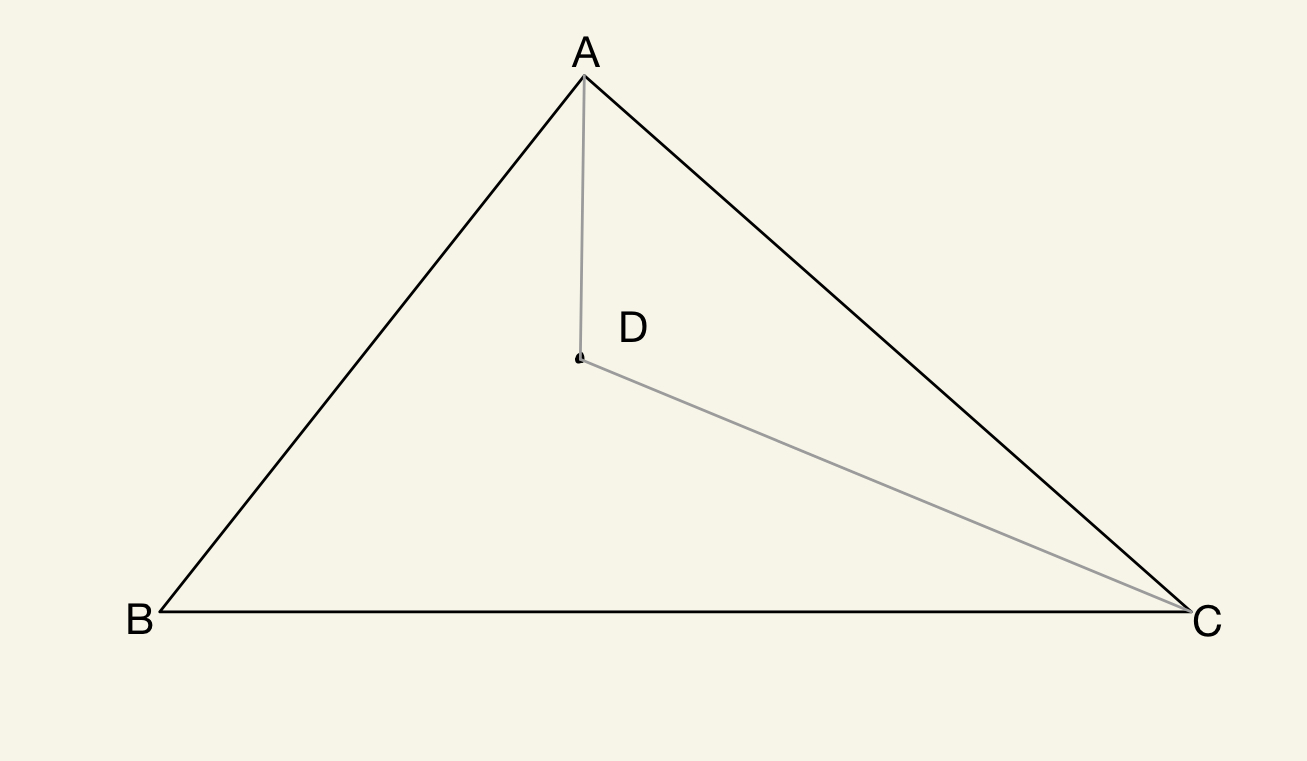Now we connect the point D and the point A, and at the same time, we connect the point D and the point C. After that, we get a new triangle with three vertices A, D, and C. But there is no points inside the new triangle which contradicts to our assumption. And hence our assumption is false. Therefore the original statement is true.

3. Prove the following by induction:
(a) is divisible by 3.
Proof: We need to prove that by induction.
For n=1, which is divisible by 3, so the identity is valid for n=1.
Assume the identity holds for n. So . Now we need to show show that . We split the into two sections i.e. . And by our assumption, we can get . It’s trivial to get . For n+1, . Hence, by induction, the theorem is proved.

(b) for all n ≥ 5.
Proof: By induction.
For n=5, the left-hand side is 720 and the right-hand side is 256, so the inequality is valid for n=5.
Assume the identity holds for n. So . Now we need to show show that . We split the into two sections i.e. . And by our assumption, we can get . And since , so . So we can get . For n+1, . Hence, by induction, the theorem is proved.

(c) ∀n ∈ N :
Proof: By induction.
For n=1, the left-hand side is and the right-hand side is , so the inequality is valid for n=1.
Assume the identity holds for n. So . Now we need to show show that . We split the into two sections i.e. . And by our assumption, we can get . By combining like items, we can get . It’s trivial to get .This is the identity for n+1. Hence, by induction, the theorem is proved.