Lecture 10B: Real Analysis 2
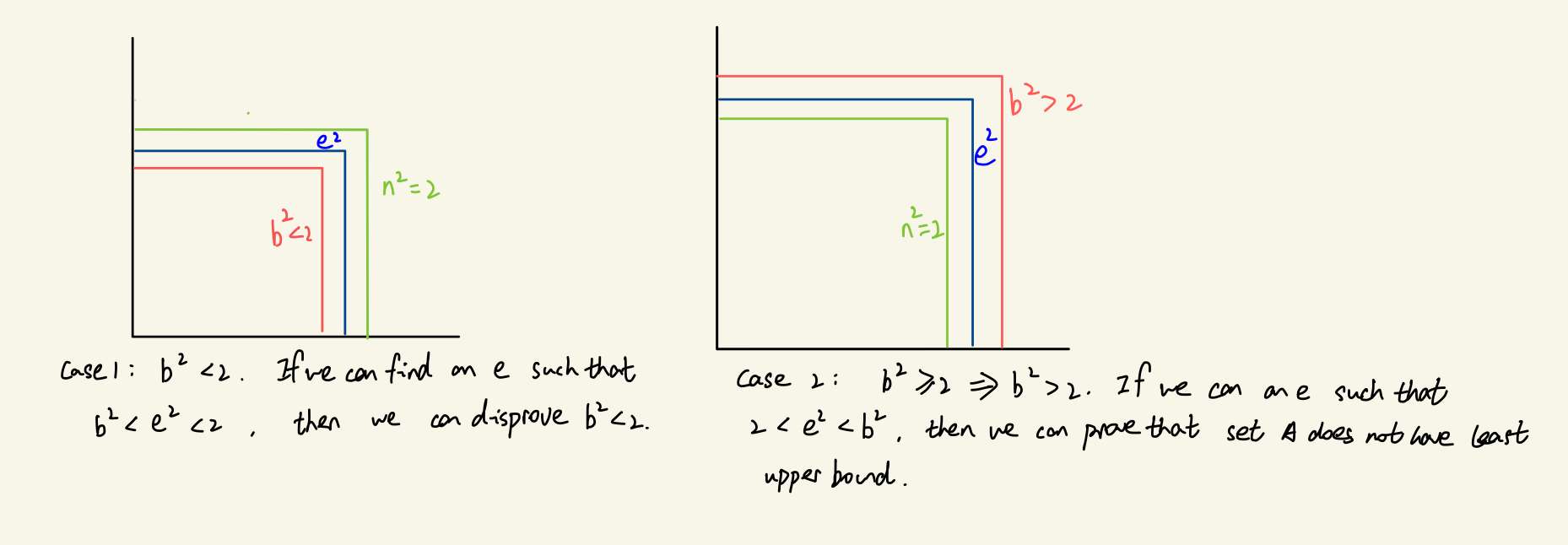
Theorem: The rational line is not complete.
Proof: By contradiction. Assume the rational line is complete.
Then there exists a counterexample. Let A={x

Supplementary Materials
https://home.iitk.ac.in/~psraj/mth101/lecture_notes/lecture1.pdf
All articles in this blog are licensed under CC BY-NC-SA 4.0 unless stating additionally.